亿万级数据处理的高效解决方案

亿万级数据处理的高效解决方案 - 知乎 (zhihu.com)

简介

全文行文是基于面试题的分析基础之上的，具体实践过程中，还是得具体情况具体分析，且各个场景下需要考虑的细节也远比本文所描述的任何一种解决方法复杂得多。

何谓海量数据处理

基于海量数据上的存储、处理、操作。

何谓海量，就是数据量太大，导致要么是无法在较短时间内迅速解决，要么是数据太大，导致无法一次性装入内存。

那解决办法呢?

针对时间，我们可以采用巧妙的算法搭配合适的数据结构，如Bloom filter/Hash/bit-map/堆/数据库或倒排索引/trie树
针对空间，无非就一个办法：大而化小，分而治之（hash映射），把规模大化为规模小的，各个击破

至于单机及集群问题，通俗点来讲

单机就是处理装载数据的机器有限(只需考虑CPU，内存，硬盘的数据交互)
集群，机器有多台，适合分布式处理，并行计算(更多考虑节点和节点间的数据交互)。

处理海量数据，不外乎

分而治之/hash映射 + hash统计 + 堆/快速/归并排序
双层桶划分
Bloom filter/Bitmap；
Trie树/数据库/倒排索引；
外排序；
分布式处理之Hadoop/Mapreduce。

本文第一部分、从set/map谈到hashtable/hash_map/hash_set，简要介绍下set/map/multiset/multimap，及hash_set/hash_map/hash_multiset/hash_multimap之区别(万丈高楼平地起，基础最重要)，而本文第二部分，则针对上述那6种方法模式结合对应的海量数据处理面试题分别具体阐述。

从set/map到hashtable/hashmap/hashset

序列式容器
vector/list/deque/stack/queue/heap
关联式容器。关联式容器又分为set(集合)和map(映射表)两大类，还有第3类关联式容器，如hashtable(散列表)
类似关联式数据库，每笔数据或每个元素都有一个键值(key)和一个实值(value)，即所谓的Key-Value(键-值对)

set/map

set，同map一样，所有元素都会根据元素的键值自动被排序，值得注意的是，两者都不允许两个元素有相同的键值。

不同的是：set的元素不像map那样可以同时拥有实值(value)和键值(key)，set元素的键值就是实值，实值就是键值，而map的所有元素同时拥有实值(value)和键值(key)，pair的第一个元素被视为键值，第二个元素被视为实值。

hash_set/hash_map

hash_set/hash_map，两者的一切操作都是基于hashtable之上。不同的是，hash_set同set一样，同时拥有实值和键值，且实质就是键值，键值就是实值，而hash_map同map一样，每一个元素同时拥有一个实值(value)和一个键值(key)，所以其使用方式，和上面的map基本相同。

但由于hash_set/hash_map都是基于hashtable之上，所以不具备自动排序功能。为什么?因为hashtable没有自动排序功能。

所以，综上什么样的结构决定其什么样的性质，因为set/map都是基于RB-tree之上，所以有自动排序功能，而hash_set/hash_map都是基于hashtable之上，所以不含有自动排序功能，至于加个前缀multi_无非就是允许键值重复而已。

秘技一:

分而治之/Hash映射 + HashMap统计 + 堆/快速/归并排序

Hash，就是把任意长度的输入（又叫做预映射， pre-image），通过散列算法，变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，而不可能从散列值来唯一的确定输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的函数。

Hash主要用于信息安全领域中加密算法，它把一些不同长度的信息转化成杂乱的128位的编码,这些编码值叫做Hash值. 也可以说，hash就是找到一种数据内容和数据存放地址之间的映射关系。

数组的特点是：寻址容易，插入和删除困难
链表的特点是：寻址困难，插入和删除容易。

那么我们能不能综合两者的特性，做出一种寻址容易，插入删除也容易的数据结构？答案是肯定的，这就是我们要提起的哈希表，哈希表有多种不同的实现方法，我接下来解释的是最常用的一种方法——拉链法，我们可以理解为“链表的数组”

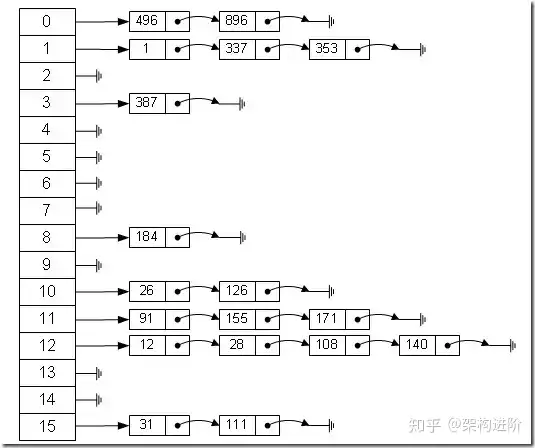
左边很明显是个数组，数组的每个成员包括一个指针，指向一个链表的头，当然这个链表可能为空，也可能元素很多。我们根据元素的一些特征把元素分配到不同的链表中去，也是根据这些特征，找到正确的链表，再从链表中找出这个元素。

元素特征转变为数组下标的方法就是散列法

除法散列法
最直观的一种，上图使用的就是这种散列法，公式：
index = value % 16
学过汇编的都知道，求模数其实是通过一个除法运算得到的，所以叫“除法散列法”。
平方散列法
求index是非常频繁的操作，而乘法的运算要比除法来得省时，所以我们考虑把除法换成乘法和一个位移操作。公式：
index = (value * value) >> 28
如果数值分配比较均匀的话这种方法能得到不错的结果，但我上面画的那个图的各个元素的值算出来的index都是0——非常失败。也许你还有个问题，value如果很大，value * value不会溢出吗？答案是会的，但我们这个乘法不关心溢出，因为我们根本不是为了获取相乘结果，而是为了获取index。
斐波那契（Fibonacci）散列法
平方散列法的缺点是显而易见的，所以我们能不能找出一个理想的乘数，而不是拿value本身当作乘数呢？答案是肯定的。
1，对于16位整数而言，这个乘数是40503
2，对于32位整数而言，这个乘数是2654435769
3，对于64位整数而言，这个乘数是11400714819323198485

这几个“理想乘数”是如何得出来的呢？这跟一个法则有关，叫黄金分割法则，而描述黄金分割法则的最经典表达式无疑就是著名的斐波那契数列，如果你还有兴趣，就到网上查找一下“斐波那契数列”等关键字，我数学水平有限，不知道怎么描述清楚为什么，另外斐波那契数列的值居然和太阳系八大行星的轨道半径的比例出奇吻合，很神奇，对么？

对我们常见的32位整数而言，公式：
index = (value * 2654435769) >> 28
如果用这种斐波那契散列法的话，那我上面的图就变成这样了：

![img](data:image/svg+xml;utf8,)

很明显，用斐波那契散列法调整之后要比原来的取模散列法好很多。

适用范围
快速查找，删除的基本数据结构，通常需要总数据量可以放入内存。
基本原理及要点
Hash函数选择，针对字符串，整数，排列，具体相应的hash方法
碰撞处理，一种是开放哈希法，亦拉链法；另一种就是closed hashing，也称开地址法，opened addressing。
扩展
d-left hashing中的d是多个的意思，我们先简化这个问题，看一看2-left hashing。2-left hashing指的是将一个哈希表分成长度相等的两半，分别叫做T1和T2，给T1和T2分别配备一个哈希函数，h1和h2。在存储一个新的key时，同时用两个哈希函数进行计算，得出两个地址h1[key]和h2[key]。这时需要检查T1中的h1[key]位置和T2中的h2[key]位置，哪一个位置已经存储的（有碰撞的）key比较多，然后将新key存储在负载少的位置。如果两边一样多，比如两个位置都为空或者都存储了一个key，就把新key 存储在左边的T1子表中，2-left也由此而来。在查找一个key时，必须进行两次hash，同时查找两个位置。

案例

海量日志数据，提取出某日访问百度次数最多的那个IP

无非分而治之/hash映射 + hash统计 + 堆/快速/归并排序，说白了，就是先映射，后统计，最后排序

分而治之/hash映射
针对数据太大，内存受限，只能把大文件化成(取模映射)小文件
HashMap统计：当大文件转化了小文件，便可以采用常规的HashMap(ip，value)进行频率统计
堆/快速排序
统计完了之后，进行排序(可采取堆排序)，得到次数最多的IP

首先是这一天，并且是访问百度的日志中的IP取出来，逐个写入到一个大文件中。

注意到IP是32位的，最多有个2^32个IP。同样可以采用映射的方法，比如%1000，把整个大文件映射为1000个小文件，再找出每个小文中出现频率最大的IP（可以采用HashMap对那1000个文件中的所有IP进行频率统计，然后依次找出各个文件中频率最大的那个IP）及相应的频率。然后再在这1000个最大的IP中，找出那个频率最大的IP，即为所求。

还有几个问题

Hash取模是一种等价映射，不会存在同一个元素分散到不同小文件中的情况，即这里采用的是mod 1000算法，那么相同的IP在hash取模后，只可能落在同一个文件中，不可能被分散
那到底什么是hash映射呢？
简单来说，就是为了便于计算机在有限的内存中处理大数据，从而通过一种映射散列的方式让数据均匀分布在对应的内存位置(如大数据通过取余的方式映射成小树存放在内存中，或大文件映射成多个小文件)，而这个映射散列方式便是我们通常所说的hash函数，好的hash函数能让数据均匀分布而减少冲突。尽管数据映射到了另外一些不同的位置，但数据还是原来的数据，只是代替和表示这些原始数据的形式发生了变化而已

堆

概念

堆是一种特殊的二叉树,具备以下两种性质

每个节点的值都大于(或者都小于，即最小堆)其子节点的值
树完全平衡的，并且最后一层的树叶都在最左边

这样就定义了一个最大堆

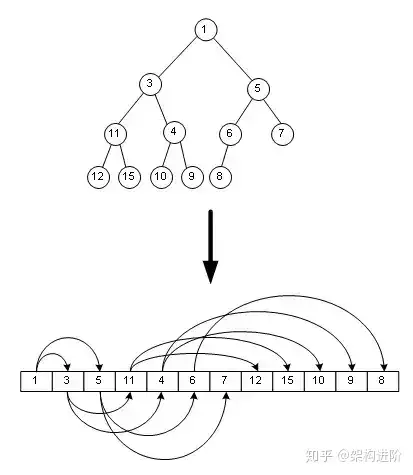
数组表示堆

二叉堆
一种完全二叉树，其任意子树的左右节点（如果有的话）的键值一定比根节点大，上图其实就是一个二叉堆

最小的一个元素就是数组第一个元素,那么二叉堆这种有序队列如何入队呢

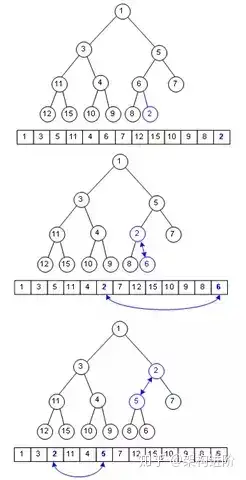
假设要在这个二叉堆里入队一个单元，键值为2，那只需在数组末尾加入这个元素，然后尽可能把这个元素往上挪，直到挪不动，经过了这种复杂度为Ο(logn)的操作，二叉堆还是二叉堆。

那如何出队呢

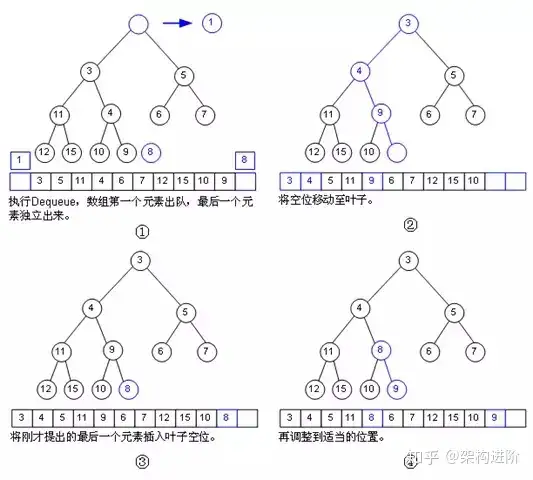
出队一定是出数组的第一个元素，这么来第一个元素以前的位置就成了空位，我们需要把这个空位挪至叶子节点，然后把数组最后一个元素插入这个空位，把这个“空位”尽量往上挪。这种操作的复杂度也是Ο(logn)

适用范围
海量数据前n大，并且n比较小，堆可以放入内存
基本原理及要点
最大堆求前n小，最小堆求前n大。方法，比如求前n小，我们比较当前元素与最大堆里的最大元素，如果它小于最大元素，则应该替换那个最大元素。这样最后得到的n个元素就是最小的n个。适合大数据量，求前n小，n的大小比较小的情况，这样可以扫描一遍即可得到所有的前n元素，效率很高。
扩展
双堆，一个最大堆与一个最小堆结合，可以用来维护中位数。

100w个数中找最大的前100个数

用一个100个元素大小的最小堆即可。

寻找热门查询，300万个查询字符串中统计最热门的10个查询

搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有一千万个记录（这些查询串的重复度比较高，虽然总数是1千万，但如果除去重复后，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就是越热门），请你统计最热门的10个查询串，要求使用的内存不能超过1G。

解答：由上题，我们知道，数据大则划为小的，如一亿个IP求Top 10，可先%1000将IP分到1000个小文件中去，并保证一种IP只出现在一个文件中，再对每个小文件中的IP进行HashMap计数统计并按数量排序，最后归并或者最小堆依次处理每个小文件的Top10以得到最后的结果

但如果数据规模比较小，能一次性装入内存呢?比如这题，虽然有一千万个Query，但是由于重复度比较高，因此事实上只有300万的Query，每个Query 255字节，因此我们可以考虑把他们都放进内存中去（300万个字符串假设没有重复，都是最大长度，那么最多占用内存3M*1K/4=0.75G。所以可以将所有字符串都存放在内存中进行处理），而现在只是需要一个合适的数据结构，在这里，HashMap绝对是我们优先的选择。

所以我们放弃分而治之hash映射的步骤，直接上hash统计，然后排序。针对此类典型的TOP K问题，采取的对策往往是：HashMap + 堆

HashMap统计
对这批海量数据预处理
维护一个Key为Query字串，Value为该串出现次数的HashMap，即HashMap(Query，Value)，每次读取一个Query，如果该字串不在HashMap中，则加入该串，并将Value设1
若该串在HashMap，则将该串的计数加一
最终我们在O(N)的时间复杂度内用HashMap完成了统计
堆排序
借助堆这个数据结构，找出Top K，时间复杂度为N*logK,即借助堆结构，我们可以在log量级的时间内查找和调整。
因此，维护一个K(该题目中是10)大小的小根堆，然后遍历300万的Query，分别和根元素进行对比。
所以，我们最终的时间复杂度是O（N） + N' * O（logK），（N为1000万，N’为300万）。
堆排序思路
维护k个元素的最小堆，即用容量为k的最小堆存储最先遍历到的k个数，并假设它们即是最大的k个数，建堆O(k),调整堆O(logk)后，有
k1>k2>...kmin(kmin设为小顶堆中最小元素)
继续遍历数列，每次遍历一个元素x，与堆顶元素比较，若x>kmin，则更新堆(x入堆，用时logk)，否则不更新堆。这样下来，总费时O（k*logk+（n-k）*logk）=O（n*logk）
此方法得益于在堆中，查找等各项操作时间复杂度均为logk
也可以采用trie树，关键字域存该查询串出现的次数，没有出现为0
最后用10个元素的最小堆来对出现频率进行排序。

有一个1G的文件,每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词

由上面那两个例题，分而治之 + hash统计 + 堆/快速排序这个套路再多多验证下。此题又是文件很大，又是内存受限,无非还是

分而治之/hash映射
顺序读文件中，对于每个词x，取hash(x)%5000,然后按照该值存到5000个小文件（记为x0,x1,…x4999）中。这样每个文件大概是200k。
如果其中的有的文件超过了1M，还可以按照类似的方法继续下分，直到分解得到的小文件都不超过1M
HashMap统计
对每个小文件，采用trie树/HashMap等统计每个文件中出现的词以及相应的频率
堆/归并排
取出出现频率最大的100个词（可以用含100个结点的最小堆）后，再把100个词及相应的频率存入文件，这样又得到了5000个文件。最后就是把这5000个文件进行归并（类似于归并排序）的过程了。

海量数据分布在10台电脑中,想个办法高效统计出这批数据的TOP10,如果每个数据元素只出现一次，而且只出现在某一台机器中，那么可以采取以下步骤统计出现次数TOP10的数据元素：

堆排序
在每台电脑上求出TOP10，可以采用包含10个元素的堆完成（TOP10小，用最大堆，TOP10大，用最小堆，比如求TOP10大，我们首先取前10个元素调整成最小堆，如果发现，然后扫描后面的数据，并与堆顶元素比较，如果比堆顶元素大，那么用该元素替换堆顶，然后再调整为最小堆。最后堆中的元素就是TOP10大）。
求出每台电脑上的TOP10后，然后把这100台电脑上的TOP10组合起来，共1000个数据，再利用上面类似的方法求出TOP10就可以了。

如果同一个元素重复出现在不同的电脑中呢

这个时候，你可以有两种方法

遍历所有数据，重新hash取模，使同一个元素只出现在单独的一台电脑中，然后采用上面所说的方法，统计每台电脑中各个元素的出现次数找出TOP10，继而组合100台电脑上的TOP10，找出最终的TOP10
暴力求解：直接统计每台电脑中各个元素的出现次数，然后把同一个元素在不同机器中的出现次数相加，最终从所有数据中找出TOP10

10个文件，每个1G，每个文件的每一行存放的都是用户的query，每个文件的query都可能重复。要求按照query的频度排序

方案1

Hash映射
顺读10个文件，按照hash(query)%10将query写到另外10个文件(记为a0,a1,..a9)中
这样新生成的文件每个的大小大约也1G)(假设hash函数较好)
HashMap统计
找一台内存在2G左右机器，依次用HashMap(query, query_count)统计每个query频度
注：HashMap(query,query_count)是统计每个query的出现次数，不是存储他们的值，出现一次，则count+1
堆/快速/归并排序
利用快速/堆/归并排序按频率排序，将排序好的query和对应的query_cout输出到文件，就得到了10个排好序的文件

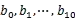
最后，对这10个文件进行归并排序（内/外排相结合）

方案2

一般query的总量是有限的，只是重复的次数比较多而已，可能对于所有的query，一次性就可以加入到内存了。这样，我们就可以采用trie树/HashMap等直接统计每个query出现的次数，然后按次数做快速/堆/归并排序

方案3

与方案1类似，但在做完hash，分成多个文件后，可以交给多个文件来处理，采用分布式的架构来处理（比如MapReduce），最后再进行合并

给定a、b两个文件，各存放50亿个url，每个url各占64字节，内存限制是4G，找出a、b文件共同的url

可估计每个文件的大小为5G×64=320G，远远大于内存限制。所以不可能将其完全加载到内存中处理。考虑采取分而治之的方法

分而治之/hash映射

遍历文件a，对每个url求取

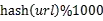
然后根据所取得的值将url分别存储到1000个小文件

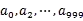
(漏个a1)中。
这样每个小文件大约300M
遍历文件b，采取和a相同方式将url分别存储到1000个小文件

![img](data:image/svg+xml;utf8,)

这样处理后，所有可能相同的url都在对应的小文件

![img](data:image/svg+xml;utf8,)

不对应的小文件不可能有相同的url。然后我们只要求出1000对小文件中相同的url即可

HashSet统计
求每对小文件中相同的url时，可以把其中一个小文件的url存储到HashSet
然后遍历另一个小文件的url，看其是否在刚才构建的HashSet中，如果是，那么就是共同的url，存到文件即可

此即第一个秘技
分而治之/hash映射 + hash统计 + 堆/快速/归并排序
再看最后4道题

在海量数据中找出重复次数最多的

先hash
然后求模映射为小文件，求出每个小文件中重复次数最多的，并记录重复次数
最后找出上一步求出的数据中重复次数最多的即为所求

千万或上亿数据（有重复）,统计次数最多的前N个数据

上千万或上亿的数据，现在的机器的内存应该能存下
考虑采用HashMap/搜索二叉树/红黑树等来进行统计次数
最后利用堆取出前N个出现次数最多的数据

一个文本文件，约一万行，每行一个词，统计出其中最频繁的10个词，给出思想及时间复杂度分析

方案1

如果文件较大,无法一次性读入内存，可采用hash取模，将大文件分解为多个小文件
对于单个小文件利用HashMap统计出每个小文件中10个最常出现的词
然后归并
找出最终的10个最常出现的词

方案2

通过hash取模将大文件分解为多个小文件后
-用trie树统计每个词出现的次数，时间复杂度O(n*le)(le:单词平均长度），最终同样找出出现最频繁的前10个词（可用堆来实现），时间复杂度是O(n*lg10)。

10. 1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。请怎么设计和实现？

方案1：这题用trie树比较合适，hash_map也行。
方案2：from xjbzju:，1000w的数据规模插入操作完全不现实，以前试过在stl下100w元素插入set中已经慢得不能忍受，觉得基于hash的实现不会比红黑树好太多，使用vector+sort+unique都要可行许多，建议还是先hash成小文件分开处理再综合。

一个文本文件，找出前10个经常出现的词，但这次文件比较长，说是上亿行或十亿行，总之无法一次读入内存，问最优解

方案1：首先根据用hash并求模，将文件分解为多个小文件，对于单个文件利用上题的方法求出每个文件件中10个最常出现的词。然后再进行归并处理，找出最终的10个最常出现的词。

100w个数中找出最大的100个数

方案1:局部淘汰法

取前100个元素，并排序，记为序列L
然后一次扫描剩余的元素x，与排好序的100个元素中最小的元素比，如果比这个最小的要大，那么把这个最小的元素删除，并把x利用插入排序的思想，插入到序列L中。依次循环，知道扫描了所有的元素。复杂度为O(100w*100)。

方案2

快速排序的思想，每次分割之后只考虑比轴大的部分，知道比轴大的一部分在比100多的时候，采用传统排序算法排序，取前100个。复杂度为O(100w*100)

方案3

在前面的题中，我们已经提到了，用一个含100个元素的最小堆完成。复杂度为O(100w*lg100)。
接下来看第二种方法，双层桶划分

秘技二:双层桶划分

一种算法设计思想。面对大量的数据我们无法处理时，可以将其分成一个个小任务，然后根据一定的策略来处理这些小任务，从而达到目的。

适用场景
第k大，中位数，不重复或重复的数字
基本原理及要点
因为元素范围很大，不能利用直接寻址表，所以通过多次划分，逐步确定范围，然后最后在一个可以接受的范围内进行。可以通过多次缩小，双层只是一个例子，分治才是其根本（只是“只分不治”）。

【扩展】 当有时候需要用一个小范围的数据来构造一个大数据，也是可以利用这种思想，相比之下不同的，只是其中的逆过程。

【问题实例】 1).2.5亿个整数中找出不重复的整数的个数，内存空间不足以容纳这2.5亿个整数。

有点像鸽巢原理，整数个数为232,也就是，我们可以将这232个数，划分为2^8个区域(比如用单个文件代表一个区域)，然后将数据分离到不同的区域，然后不同的区域在利用bitmap就可以直接解决了。也就是说只要有足够的磁盘空间，就可以很方便的解决。当然这个题也可以用我们前面讲过的BitMap方法解决，正所谓条条大道通罗马~~~

2).5亿个int找它们的中位数。

这个例子比上面那个更明显。首先我们将int划分为2^16个区域，然后读取数据统计落到各个区域里的数的个数，之后我们根据统计结果就可以判断中位数落到那个区域，同时知道这个区域中的第几大数刚好是中位数。然后第二次扫描我们只统计落在这个区域中的那些数就可以了。

实际上，如果不是int是int64，我们可以经过3次这样的划分即可降低到可以接受的程度。即可以先将int64分成2^24个区域，然后确定区域的第几大数，在将该区域分成220个子区域，然后确定是子区域的第几大数，然后子区域里的数的个数只有220，就可以直接利用direct addr table进行统计了。

3).现在有一个0-30000的随机数生成器。请根据这个随机数生成器，设计一个抽奖范围是0-350000彩票中奖号码列表，其中要包含20000个中奖号码。

这个题刚好和上面两个思想相反，一个0到3万的随机数生成器要生成一个0到35万的随机数。那么我们完全可以将0-35万的区间分成35/3=12个区间，然后每个区间的长度都小于等于3万，这样我们就可以用题目给的随机数生成器来生成了，然后再加上该区间的基数。那么要每个区间生成多少个随机数呢？计算公式就是：区间长度随机数密度，在本题目中就是30000（20000/350000）。最后要注意一点，该题目是有隐含条件的：彩票，这意味着你生成的随机数里面不能有重复，这也是我为什么用双层桶划分思想的另外一个原因。

其本质上还是分而治之思想,重在”分”

适用范围：第k大，中位数，不重复或重复的数字
基本原理及要点：元素范围很大，不能利用直接寻址表，所以多次划分，逐步确定范围，然后最后在一个可以接受的范围内进行

2.5亿个整数中找出不重复的整数的个数，内存空间不足以容纳这2.5亿个整数

整数个数为2^32, 也就是，我们可以将这232个数,划分为28个区域(如用单个文件代表一个区域),然后将数据分离到不同的区域，然后不同的区域再利用bitmap(https://www.jianshu.com/p/a0294f9a321e)就可直接解决
也就是说只要有足够的磁盘空间，就可以很方便的解决。

5亿个int找它们的中位数

思路一

将int划分为2^16个区域
读取数据,统计落到各个区域里的数的个数
根据统计结果判断中位数落到哪个区域,同时知道这个区域中的第几大数刚好是中位数
第二次扫描,只统计落在这个区域中的那些数即可

实际上，如果是long，我们可以经过3次这样的划分即可降低到可以接受的程度
即可以先将long分成224个区域，然后确定区域的第几大数，在将该区域分成220个子区域，然后确定是子区域的第几大数，然后子区域里的数的个数只有2^20，就可以直接利用direct addr table进行统计了。

思路二

同样需要做两遍统计，如果数据存在硬盘上，就需要读取2次
方法同基排，开一个大小为65536的Int数组，第一遍读取，统计Int的高16位，也就是

0-65535，都算作0
65536 - 131071都算作1
就相当于用该数除以65536
Int除以 65536的结果不会超过65536种情况，因此开一个长度为65536的数组计数即可
每读取一个数，数组中对应计数+1，考虑有负数的情况，需要将结果加32768(因为只用一半)后，记录在相应的数组内。

第一遍统计之后，遍历数组累加，看中位数处于哪个区间
比如处于区间k，那么0~k-1内数字的数量sum应该<n/2（2.5亿）
而k+1 ~ 65535的计数和也<n/2

第二遍统计同上面方法，但这次只统计处于区间k的情况，也就是说(x / 65536) + 32768 = k。统计只统计低16位的情况。并且利用刚才统计的sum，比如sum = 2.49亿，那么现在就是要在低16位里面找100万个数(2.5亿-2.49亿)。这次计数之后，再统计一下，看中位数所处的区间，最后将高位和低位组合一下就是结果

秘技三：Bloom filter/Bitmap

Bloom filter

适用范围
可以用来实现数据字典，数据判重，集合求交集
基本原理及要点
对于原理来说很简单，位数组+k个独立hash函数。
将Hash函数对应的值的位数组置1，查找时如果发现所有Hash函数对应位都是1说明存在
很明显这个过程并不保证查找的结果100%正确的。
同时也不支持删除一个已经插入的关键字，因为该关键字对应的位会牵动到其他的关键字。
所以一个简单的改进就是 counting Bloom filter，用一个counter数组代替位数组，就可以支持删除了
Bloom filter将集合中的元素映射到位数组中，用k(哈希函数个数)个映射位是否全1表元素是否在该集合
Counting bloom filter（CBF）将位数组中的每一位扩展为一个counter，从而支持了元素的删除操作。Spectral Bloom Filter（SBF）将其与集合元素的出现次数关联。SBF采用counter中的最小值来近似表示元素的出现频率。

A,B两个文件，各存放50亿条URL，每条URL占用64B，内存限制4G，求A,B文件URL交集。如果是三个乃至n个文件呢

先计算下内存占用，4G=2^32大概40亿*8大概340亿bit
n=50亿，若按出错率0.01算需要大概650亿bit
现在可用340亿，相差不多，可能会使出错率上升
另外如果这些url与ip是一一对应的，就可以转换成ip，则大大简单了

同时本题若允许有一定的错误率，可使用Bloom filter
将其中一个文件中的url使用Bloom filter映射为340亿bit，然后挨个读取另外一个文件的url，检查是否在Bloom filter，如果是，那么该url应该是共同的url（注意会有一定的错误率）

BitMap

用一个bit位标记某个元素对应的Value，而Key即是该元素

由于采用了bit为单位来存储数据，因此在存储空间方面，相对于 HashMap大大节省

看一个具体的例子，假设我们要对0-7内的5个元素(4,7,2,5,3)排序（假设这些元素没有重复）。

要表示8个数,我们就只需要8个Bit(1Byte),首先我们开辟1Byte的空间，将这些空间的所有Bit位都置为0

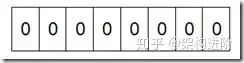
然后遍历这5个元素，首先第一个元素是4，那么就把4对应的位置为1,因为是从0开始的，所以要把第5位置1

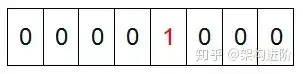
然后遍历一遍bit区域，将是1的位的编号输出（2，3，4，5，7），就达到了排序的目的。下面的代码给出了一个BitMap的用法：排序

//定义每个Byte中有8个Bit位#include ＜memory.h＞#define BYTESIZE 8void SetBit(char *p, int posi){    for(int i=0; i ＜ (posi/BYTESIZE); i++)
   {
       p++;
   }

   *p = *p|(0x01＜＜(posi%BYTESIZE));//将该Bit位赋值1
   return;
}
void BitMapSortDemo(){    //为了简单起见，我们不考虑负数
   int num[] = {3,5,2,10,6,12,8,14,9};
   //BufferLen这个值是根据待排序的数据中最大值确定的
   //待排序中的最大值是14，因此只需要2个Bytes(16个Bit)
   //就可以了。
   const int BufferLen = 2;    char *pBuffer = new char[BufferLen];
   //要将所有的Bit位置为0，否则结果不可预知。
   memset(pBuffer,0,BufferLen);    for(int i=0;i＜9;i++)
   {        //首先将相应Bit位上置为1
       SetBit(pBuffer,num[i]);
   }
   //输出排序结果
   for(int i=0;i＜BufferLen;i++)//每次处理一个字节(Byte)
   {        for(int j=0;j＜BYTESIZE;j++)//处理该字节中的每个Bit位
       {            //判断该位上是否是1，进行输出，这里的判断比较笨。
           //首先得到该第j位的掩码（0x01＜＜j），将内存区中的
           //位和此掩码作与操作。最后判断掩码是否和处理后的
           //结果相同
           if((*pBuffer&amp;(0x01＜＜j)) == (0x01＜＜j))
           {                printf("%d ",i*BYTESIZE + j);
           }
       }
       pBuffer++;
   }
}
int _tmain(int argc, _TCHAR* argv[])
{
   BitMapSortDemo();    return 0;
}

适用范围
可进行数据的快速查找，判重，删除，一般来说数据范围是int的10倍以下
基本原理及要点
使用bit数组来表示某些元素是否存在，比如8位电话号码
扩展
Bloom filter可以看做是对BitMap的扩展

已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数

8位最多99 999 999，大概需要99m个bit，大概十几M字节的内存即可(可理解为从0~99 999 999的数字,每个数字对应一个bit位,所以只需要99M个bit约12.4M的Bytes,这样就用了小小的12.4M左右的内存表示了所有的8位数的电话)

在2.5亿个整数中找出不重复的整数，注，内存不足以容纳这2.5亿个整数

方案1

采用2-BitMap,每个数分配2bit

00表示不存在
01表示出现一次
10表示多次
11无意义

共需内存2^32 * 2 bit=1 GB,尚可接受

然后扫描这2.5亿个整数，查看BitMap中相应位，如果是00变01，01变10，10保持不变。

扫荡完毕后,查看BitMap,把对应位是01的整数输出即可

方案2

也可采用与第1题类似的方法，进行划分小文件的方法。然后在小文件中找出不重复的整数，并排序。然后再进行归并，注意去除重复的元素

40亿个不重复的非负int的整数，没排过序，然后再给一个数，如何快速判断这个数是否在那40亿个数当中

申请512M内存，一个bit位代表一个int非负值。读入40亿个数，设置相应的bit位，读入要查询的数，查看相应bit位是否为1，为1表示存在，为0表示不存在。

秘技四 Trie树/数据库/倒排索引

Trie树

适用范围
数据量大，重复多，但数据种类少可放入内存
基本原理及要点
实现方式，节点孩子的表示方式
扩展
压缩实现

一个文本文件，大约一万行，每行一个词，要求统计出其中最频繁出现的前10个词

用trie树统计每个词出现的次数，时间复杂度是O(n*le)（le表示单词的平准长度），然后找出出现最频繁的10个

数据库索引

适用范围
大数据量的增删改查
基本原理及要点
利用数据的设计实现方法，对海量数据的增删改查

倒排索引(Inverted index)

适用范围
搜索引擎，关键字查询
基本原理及要点
为何叫倒排索引？一种索引方法，被用来存储在全文搜索下某个单词在一个文档或者一组文档中的存储位置的映射。
以英文为例，下面是要被索引的文本：

1
2
3

T0 = "it is what it is"
T1 = "what is it"
T2 = "it is a banana"

我们就能得到下面的反向文件索引

"a":      {2}
   "banana": {2}
   "is":     {0, 1, 2}
    "it":     {0, 1, 2}
    "what":   {0, 1}

检索的条件”what”,”is”和”it”将对应集合的交集。

正向索引开发出来用来存储每个文档的单词的列表。正向索引的查询往往满足每个文档有序频繁的全文查询和每个单词在校验文档中的验证这样的查询。在正向索引中，文档占据了中心的位置，每个文档指向了一个它所包含的索引项的序列。也就是说文档指向了它包含的那些单词，而反向索引则是单词指向了包含它的文档，很容易看到这个反向的关系。
　　扩展：
　　问题实例：文档检索系统，查询那些文件包含了某单词，比如常见的学术论文的关键字搜索。

秘技五外排序

适用范围
大数据的排序，去重
基本原理及要点
外排序的归并方法，置换选择败者树原理，最优归并树

1G大小的一个文件，每一行一个词，词大小不超过16B，内存限制大小是1M。返回频数最高的100词

这个数据具有很明显的特点，词的大小为16B，但内存只有1M,做hash明显不够，所以可以用来排序。内存可以当输入缓冲区使用。

秘技六 MapReduce

计算模型，简单的说就是将大批量的工作（数据）分解（MAP）执行，然后再将结果合并成最终结果（REDUCE）。这样做的好处是可以在任务被分解后，可以通过大量机器进行并行计算，减少整个操作的时间原理就是一个归并排序。

适用范围
数据量大，但是数据种类小可以放入内存
基本原理及要点
将数据交给不同的机器去处理，数据划分，结果归约给读者看最后一道题，如下：

非常大的文件，装不进内存。每行一个int类型数据，现在要你随机取100个数。

发现上述这道题，无论是以上任何一种模式/方法都不好做，那有什么好的别的方法呢？我们可以看看：操作系统内存分页系统设计(说白了，就是映射+建索引)。

Windows 2000使用基于分页机制的虚拟内存。每个进程有4GB的虚拟地址空间。基于分页机制，这4GB地址空间的一些部分被映射了物理内存，一些部分映射硬盘上的交换文件，一些部分什么也没有映射。程序中使用的都是4GB地址空间中的虚拟地址。而访问物理内存，需要使用物理地址。关于什么是物理地址和虚拟地址，请看：

物理地址 (physical address): 放在寻址总线上的地址。放在寻址总线上，如果是读，电路根据这个地址每位的值就将相应地址的物理内存中的数据放到数据总线中传输。如果是写，电路根据这个地址每位的值就将相应地址的物理内存中放入数据总线上的内容。物理内存是以字节(8位)为单位编址的。
虚拟地址 (virtual address): 4G虚拟地址空间中的地址，程序中使用的都是虚拟地址。使用了分页机制之后，4G的地址空间被分成了固定大小的页，每一页或者被映射到物理内存，或者被映射到硬盘上的交换文件中，或者没有映射任何东西。对于一般程序来说，4G的地址空间，只有一小部分映射了物理内存，大片大片的部分是没有映射任何东西。物理内存也被分页，来映射地址空间。对于32bit的 Win2k，页的大小是4K。CPU用来把虚拟地址转换成物理地址的信息存放在叫做页目录和页表的结构里。
物理内存分页，一个物理页的大小为4K字节，第0个物理页从物理地址 0x00000000 处开始。由于页的大小为4KB，就是0x1000字节，所以第1页从物理地址 0x00001000 处开始。第2页从物理地址 0x00002000 处开始。可以看到由于页的大小是4KB，所以只需要32bit的地址中高20bit来寻址物理页。
返回上面我们的题目：非常大的文件，装不进内存。每行一个int类型数据，现在要你随机取100个数。针对此题，我们可以借鉴上述操作系统中内存分页的设计方法，做出如下解决方案：

OS中的方法，先生成4G的地址表，在把这个表划分为小的4M的小文件做个索引，二级索引。30位前十位表示第几个4M文件，后20位表示在这个4M文件的第几个，等等，基于key value来设计存储，用key来建索引。

http://example.com/2023/09/12/业务/亿万级数据处理的高效解决方案/

作者

where

发布于

2023年9月12日

许可协议

Java核心技术卷1 - 基础知识上一篇

COLA-项目下一篇

亿万级数据处理的高效解决方案

简介

何谓海量数据处理

从set/map到hashtable/hashmap/hashset

set/map

hash_set/hash_map

秘技一:

案例

海量日志数据，提取出某日访问百度次数最多的那个IP

堆

概念

100w个数中找最大的前100个数

寻找热门查询，300万个查询字符串中统计最热门的10个查询

有一个1G的文件,每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词

海量数据分布在10台电脑中,想个办法高效统计出这批数据的TOP10,如果每个数据元素只出现一次，而且只出现在某一台机器中，那么可以采取以下步骤统计出现次数TOP10的数据元素：

如果同一个元素重复出现在不同的电脑中呢

10个文件，每个1G，每个文件的每一行存放的都是用户的query，每个文件的query都可能重复。要求按照query的频度排序

方案1

方案2

方案3

给定a、b两个文件，各存放50亿个url，每个url各占64字节，内存限制是4G，找出a、b文件共同的url

在海量数据中找出重复次数最多的

千万或上亿数据（有重复）,统计次数最多的前N个数据

一个文本文件，约一万行，每行一个词，统计出其中最频繁的10个词，给出思想及时间复杂度分析

方案1

方案2

一个文本文件，找出前10个经常出现的词，但这次文件比较长，说是上亿行或十亿行，总之无法一次读入内存，问最优解

100w个数中找出最大的100个数

方案1:局部淘汰法

方案2

方案3

秘技二:双层桶划分

2.5亿个整数中找出不重复的整数的个数，内存空间不足以容纳这2.5亿个整数

5亿个int找它们的中位数

思路一

思路二

秘技三：Bloom filter/Bitmap

Bloom filter

A,B两个文件，各存放50亿条URL，每条URL占用64B，内存限制4G，求A,B文件URL交集。如果是三个乃至n个文件呢

BitMap

已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数

在2.5亿个整数中找出不重复的整数，注，内存不足以容纳这2.5亿个整数

方案1

方案2

40亿个不重复的非负int的整数，没排过序，然后再给一个数，如何快速判断这个数是否在那40亿个数当中

秘技四 Trie树/数据库/倒排索引

Trie树

一个文本文件，大约一万行，每行一个词，要求统计出其中最频繁出现的前10个词

数据库索引

倒排索引(Inverted index)

秘技五 外排序

1G大小的一个文件，每一行一个词，词大小不超过16B，内存限制大小是1M。返回频数最高的100词

秘技六 MapReduce

非常大的文件，装不进内存。每行一个int类型数据，现在要你随机取100个数。

秘技五外排序